IBM® SPSS® Amos™ 28

This section describes Amos's implementation of the Metropolis algorithm, a type of Markov chain Monte Carlo (MCMC) algorithm.

Notation

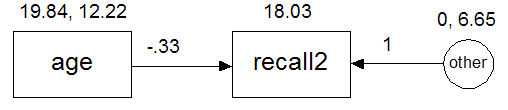
Let 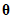contain the model parameters. To be concrete, take the following model for the attg_yng.sav data, in which age is used to predict memory performance after training (recall2).

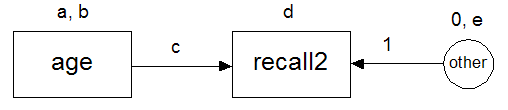
The model has five parameters: one mean (a), two variances (b and e), a regression weight (c) and an intercept (d), so has five elements,

.

The maximum likelihood estimates can be displayed on the path diagram, as shown here,

or as the vector,

.

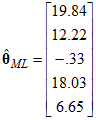The "hat" over means that contains estimates of the parameters and not the true parameter values.

Sampling from the posterior distribution of the parameters

An MCMC algorithm (such as a Metropolis algorithm) generates a sequence of parameter vectors drawn from the posterior distribution of . Here is a portion of the sequence generated by Amos's MCMC algorithm when fitting the above model.

It is typical to run the MCMC algorithm until the sequence contains many thousands of vectors. To get an idea of how such a sequence can be used to make inferences about 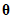, notice that in the short sequence shown above, sampled values for the mean of age are all close to 20. If this pattern holds up over a lengthy sequence you can conclude that the true mean of age in the population is close to 20. To be more precise, pick an age interval, say from 20 years to 22 years. The probability that the mean age in the population is between 20 and 22 is the same as the probability that an MCMC-generated 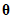will have a number between 20 and 22 as its first element. You can estimate that probability by generating a long sequence of 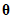vectors and calculating the proportion of those vectors that contain a number between 20 and 22 as the first element.

MCMC algorithms

Several MCMC algorithms have been proposed for generating the sequence, 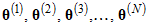. An MCMC algorithm begins with an initial parameter vector, 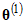. Amos sets 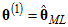. (But see the later section called Pre-burn-in.) The algorithm consists of a rule for moving from one member of the sequence to the next. Using 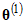as a starting point, the algorithm generates 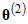, using 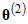it generates 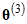, and so on.

Metropolis algorithms

Amos implements a type of MCMC algorithm known as a Metropolis algorithm. In a Metropolis algorithm, generating 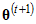from 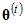is a two stage process. In the first stage, a candidate vector, 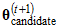is generated. In Amos, the candidate vector is generated as 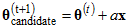, where

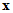▪ is a normally distributed random vector with mean 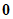and covariance matrix equal to the estimated parameter covariance matrix obtained from the information matrix after using maximum likelihood to fit the model.

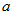▪ is the "tuning parameter" whose value you can specify on the MCMC tab in the Bayesian SEM Options window. Large values of 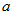tend to result in larger moves from 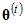to 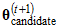. The default value for 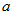is .7.

In the second stage of a Metropolis algorithm, the candidate vector is either accepted, in which case 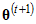is set equal to 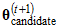, or it is rejected, in which case 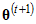is set equal to 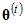. In the sequence shown earlier, it appears that 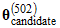was accepted because 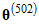is different from 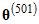. On the other hand, it appears that 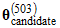and 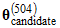were rejected because 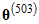and 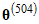are each equal to 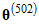. Whether a candidate vector is accepted depends on its posterior probability. Letting 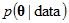stand for the posterior distribution of 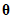, 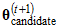is accepted or rejected according to the rule

▪Reject 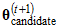if =0. In other words, always reject a 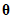that has a posterior probability density of zero.

▪Accept 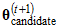if >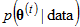. In other words, always accept a move to any new 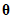that has higher posterior probability density than the current .

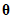▪If 0 < < 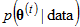, accept 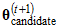with probability .

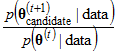Burn-in

Because 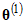is not drawn from the posterior distribution of 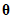, it is customary to discard the early part of the sequence, 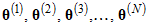. By default, Amos discards 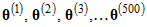, called the burn-in sample, and uses 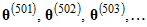(the analysis sample) to draw inferences about the posterior distribution of 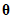. You can change the number of burn-in samples on the MCMC tab of the Bayesian SEM Options window.

Pre-burn-in

It can happen that 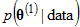=0, and that the Metropolis algorithm starts out by rejecting a very large number of candidates before eventually accepting one. This can happen, for example, if the maximum likelihood estimate, 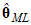, is inadmissible and there is a check mark next to Admissibility test on the Prior tab of the Bayesian SEM Options window. Because of the possibility of a long run of rejected candidates at the beginning, Amos discards every sample until it first accepts a candidate. At that point, the samples are renumbered so that the first accepted candidate becomes 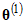. During the pre-burn-in period, the message Waiting to accept a transition before beginning burn-in is displayed in the lower-right corner of the screen.