IBM® SPSS® Amos™ 28

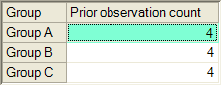
This dialog allows you to specify the Dirichlet distribution that is employed as the prior distribution of the group proportions. The following figure shows the default Dirichlet parameters for a three-group mixture modeling analysis. The default prior distribution of the three group proportions is Dirichlet with parameters (4, 4, 4). The Dirichlet parameters are referred to in the dialog box as prior observations counts because they can be interpreted in the following way.

Suppose that the number of cases in the dataset is, say, 150. Suppose that the MCMC algorithm assigns 41 cases to Group A, 45 to Group B, and 64 to Group C. Then at the next step in the MCMC algorithm the three group proportions will be sampled from the (posterior) Dirichlet distribution with parameters (4+41, 4+45, 4+64).

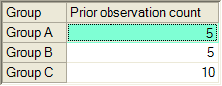
The Dirichlet parameters do not have to be equal. The following figure specifies a prior distribution according to which the proportion of the population in Group C is probably higher than the proportion in Group A or the proportion in Group B. If the sample size is much larger than 5+5+10, the prior distribution will have little effect on the posterior distribution.

If you are certain that 25% of the population is in Group A, 25% is in Group B, and 50% is in Group C, you can choose relatively large values for the prior observation counts while keeping them in the ratios 25-25-50, such as the following.

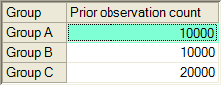
Then in the same situation imagined above, where the MCMC algorithm assigns 41 cases to Group A, 45 cases to Group B, and 64 cases to Group C, the group proportions will be sampled from the (posterior) Dirichlet distribution with parameters (10000+41, 10000+45, 20000+64). The prior observation counts will dominate the posterior distribution, and the sample group proportions will almost certainly be close to .25, .25 and .50.