IBM® SPSS® Amos™ 28

In the example, NormalityCheck produces the following output.

Assessment of normality (Group number 1)

The first row of the table shows that the lowest wordmean score was 2 and the highest was 41. wordmean had a sample skewness of

,

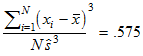where 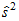is the unbiased variance estimate 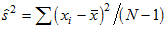. Assuming normality, skewness has a mean of zero and a standard error of 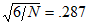. The critical ratio 2.004 in the c.r. column is the sample skewness divided by its standard error.

wordmean has a sample kurtosis of

.

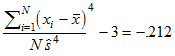Assuming normality, kurtosis has a mean of zero and a standard error of 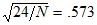. The critical ratio, –.370, is the sample kurtosis divided by its standard error.

The table has a separate row for each observed variable. A final row, labeled 'multivariate', contains Mardia's (Mardia, 1970; Mardia, 1974) coefficient of multivariate kurtosis

,

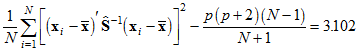where 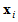is the i-th observation on the p observed variables, 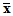is the vector of their means and 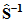is the unbiased estimate of their population covariance matrix. Assuming normality, this coefficient has a mean of zero and a standard error of 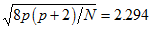. The critical ratio obtained by dividing the sample coefficient by its standard error is 1.353, as shown in the c.r. column.

Assuming normality in very large samples, each of the critical values shown in the table above is an observation on a standard normally distributed random variable. Even with a very large sample, however, the table is of limited use. All it does is to quantify the departure from normality in the sample and provide a rough test of whether the departure is statistically significant. Unfortunately, this is not enough. In order to make use of this information you also need to know how robust your chosen estimation method is against the departure from normality that you have discovered. A departure from normality that is big enough to be significant could still be small enough to be harmless.

The following table, also produced by NormalityCheck from the Grnt_fem data, provides additional evidence on the question of normality.

Observations farthest from the centroid (Mahalanobis distance) (Group number 1)

Only the first five rows of the table are shown here. Specifically, the table focuses on the occurrence of outliers, individual observations that differ markedly from the general run of observations. The table lists the observations that are furthest from the centroid of all observations, using as the distance measure for the i-th observation the squared Mahalanobis distance, 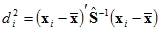. Mardia's coefficient of multivariate kurtosis can be written . The first row of the table shows that observation number 42 is furthest from the centroid with 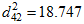. The p1 column shows that, assuming normality, the probability of 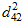(or any individual 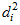) exceeding 18.747 is .005. The p2 column shows, still assuming normality, that the probability is .268 that the largest 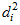would exceed 18.747. The second row of the table shows that: Observation number 20 is the second furthest observation from the centroid with 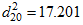. The probability of any arbitrary 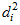exceeding 17.201 is .009. The probability of the second largest 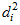exceeding 17.201 is .130. Small numbers in the p1 column are to be expected. Small numbers in the p2 column, on the other hand, indicate observations that are improbably far from the centroid under the hypothesis of normality. For the Grnt_fem data, none of the probabilities in the p2 column is very small, so there is no evidence that any of the five most unusual observations should be treated as outliers under the assumption of normality. See Bollen (1987) for a discussion of the importance of checking for outliers.