IBM® SPSS® Amos™ 28
The Bentler-Bonett (Bentler & Bonett, 1980) normed fit index ( NFI), or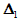 
in the notation of Bollen (1989b) can be written
,
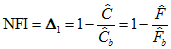where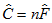 
is the minimum discrepancy of the model being evaluated and 
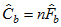is the minimum discrepancy of the baseline model.
In Example 6 the independence model can be obtained by adding constraints to any of the other models. Any model can be obtained by constraining the saturated model. So Model A, for instance, with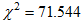 
, is unambiguously "in between" the perfectly fitting saturated model (
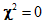) and the independence model 
).
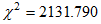Model |
NPAR |
CMIN |
DF |
P |
CMIN/DF |
Model A: No Autocorrelation |
15 |
71.544 |
6 |
.000 |
11.924 |
Model B: Most General |
16 |
6.383 |
5 |
.271 |
1.277 |
Model C: Time-Invariance |
13 |
7.501 |
8 |
.484 |
.938 |
Model D: A and C Combined |
12 |
73.077 |
9 |
.000 |
8.120 |
Saturated model |
21 |
.000 |
0 |
|
|
Independence model |
6 |
2131.790 |
15 |
.000 |
142.119 |
Looked at in this way, the fit of Model A is a lot closer to the fit of the saturated model than it is to the fit of the independence model. In fact you might say that Model A has a discrepancy that is 96.6% of the way between the (terribly fitting) independence model and the (perfectly fitting) saturated model:
.
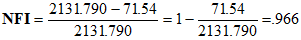Rule of thumb:
"Since the scale of the fit indices is not necessarily easy to interpret (e.g., the indices are not squared multiple correlations), experience will be required to establish values of the indices that are associated with various degrees of meaningfulness of results. In our experience, models with overall fit indices of less than .9 can usually be improved substantially. These indices, and the general hierarchical comparisons described previously, are best understood by examples." (Bentler & Bonett, 1980, p. 600, referring to both the NFI and the TLI)
Use the \nfi text macro to display NFI on a path diagram.
