IBM® SPSS® Amos™ 28

P is the probability of getting as large a discrepancy as occurred with the present sample (under appropriate distributional assumptions and assuming a correctly specified model). That is, P is a "p value" for testing the hypothesis that the model fits perfectly in the population.

One approach to model selection employs statistical hypothesis testing to eliminate from consideration those models that are inconsistent with the available data. Hypothesis testing is a widely accepted procedure and there is a lot of experience in its use. However, its unsuitability as a device for model selection was pointed out early in the development of analysis of moment structures (Jöreskog, 1969). It is generally acknowledged that most models are useful approximations that do not fit perfectly in the population. In other words, the null hypothesis of perfect fit is not credible to begin with and will in the end be accepted only if the sample is not allowed to get too big.

If you encounter resistance to the foregoing view of the role of hypothesis testing in model fitting, the following quotations may come in handy. The first two quotes predate the development of structural modeling, and refer to other model fitting problems.

▪"The power of the test to detect an underlying disagreement between theory and data is controlled largely by the size of the sample. With a small sample an alternative hypothesis which departs violently from the null hypothesis may still have a small probability of yielding a significant value of 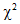. In a very large sample, small and unimportant departures from the null hypothesis are almost certain to be detected." (Cochran, 1952)

▪"If the sample is small then the 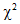test will show that the data are 'not significantly different from' quite a wide range of very different theories, while if the sample is large, the 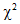test will show that the data are significantly different from those expected on a given theory even though the difference may be so very slight as to be negligible or unimportant on other criteria." (Gulliksen & Tukey, 1958, pp. 95–96)

▪"Such a hypothesis [of perfect fit] may be quite unrealistic in most empirical work with test data. If a sufficiently large sample were obtained this 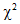statistic would, no doubt, indicate that any such non-trivial hypothesis is statistically untenable." (Jöreskog, 1969, p. 200)

▪"... in very large samples virtually all models that one might consider would have to be rejected as statistically untenable .... In effect, a nonsignificant chi-square value is desired, and one attempts to infer the validity of the hypothesis of no difference between model and data. Such logic is well-known in various statistical guises as attempting to prove the null hypothesis. This procedure cannot generally be justified, since the chi-square variate v can be made small by simply reducing sample size." (Bentler & Bonett, 1980, p. 591)

▪"Our opinion ... is that this null hypothesis [of perfect fit] is implausible and that it does not help much to know whether or not the statistical test has been able to detect that it is false." (Browne & Mels, 1992, p. 78).

See PCLOSE.

Use the \p text macro to display P on a path diagram.