IBM® SPSS® Amos™ 28

The RMR (root mean square residual) is the square root of the average squared amount by which the sample variances and covariances differ from their estimates obtained under the assumption that your model is correct:

.

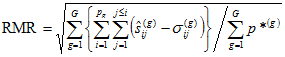The smaller the RMR is, the better. An RMR of zero indicates a perfect fit.

The following output from Example 6 shows that, according to the RMR, Model D is the best among the models considered except for the saturated model:

Use the \rmr text macro to display RMR on a path diagram.