IBM® SPSS® Amos™ 28

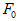incorporates no penalty for model complexity and will tend to favor models with many parameters. In comparing two nested models, 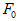will never favor the simpler model. Steiger and Lind (1980) suggested compensating for the effect of model complexity by dividing 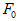by the number of degrees of freedom for testing the model. Taking the square root of the resulting ratio gives the population "root mean square error of approximation", called RMS by Steiger and Lind, and RMSEA by Browne and Cudeck (1993).

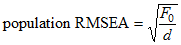
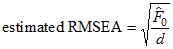
The columns labeled LO 90 and HI 90 contain the lower limit and upper limit of a 90% confidence interval for the population value of RMSEA. The limits are given by

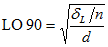
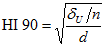
Rule of thumb:

"Practical experience has made us feel that a value of the RMSEA of about .05 or less would indicate a close fit of the model in relation to the degrees of freedom. This figure is based on subjective judgment. It cannot be regarded as infallible or correct, but it is more reasonable than the requirement of exact fit with the RMSEA = 0.0. We are also of the opinion that a value of about 0.08 or less for the RMSEA would indicate a reasonable error of approximation and would not want to employ a model with a RMSEA greater than 0.1." (Browne and Cudeck, 1993)

Use the \rmsea text macro to display RMSEA on a path diagram. Use \rmsealo and \rmseahi to display the lower and upper limits of the 90% confidence interval.