IBM® SPSS® Amos™ 28

Amos uses the method of batch means to calculate S.E., an estimate of the Monte Carlo standard error. The present topic describes the calculation of S.E.

Using the notation from the topic How the MCMC algorithm works, let 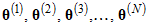be the sequence of parameter vectors generated by the MCMC algorithm.

Let 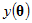be some scalar function of the model parameters. 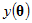can be an element of 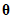such as a regression weight or the covariance between two exogenous variables. It can also be some more complicated function of the parameters such as a correlation or an indirect effect. Finally, 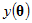can be a user-defined custom estimand.

Let B be the number of burn-in observations so that the posterior mean of 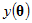is estimated by .

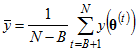The method of batch means begins by breaking up the N-B post-burn-in observations into m consecutive batches of n observations, and computing a mean within each batch as follows:

, , , ...,

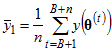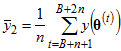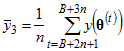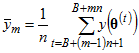
It may not be possible to choose m and n so that B+mn = N. In that case m and n are chosen so that B+mn is as large as possible while not exceeding N. The 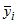are the "batch means". Let 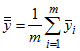be the mean of the batch means. If n is sufficiently large that the 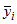are approximately independent, then

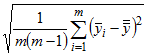
is an estimate of the standard error of 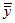. Since 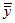is the mean of a sample of mn observations and 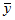is the mean of N-B observations, Amos estimates the standard error of 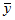as

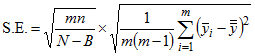
By default, the number of batches, m, is 20. Amos then chooses n to be as large as possible without making 20n exceed N-B. You can change the number of batches on the MCMC tab of the Bayesian SEM Options window.