IBM® SPSS® Amos™ 28

With three categories, there are two category boundaries. This presents the simplest situation for estimating category boundaries, because for most models the values assigned to the boundaries do not matter.

Summary

For a three-category variable, substituting one pair of boundary values for another amounts to performing a linear transformation on the underlying numeric variable. The effect on model fit and on parameter estimates is the same as if a linear transformation is performed on a directly observed numeric variable. For most models, model fit is unaffected and parameter estimates are transformed in such a way as to leave their interpretation unaffected. This means that for such models, called invariant under changes of scale and location by Browne (1982), the boundaries can be chosen arbitrarily.

As noted below, it is sometimes important to make sure that several three-category variables all use the same values for the two boundaries.

For three-category variables, Amos sets the two boundaries to 0 and 1. To use different values, click the Details button in the Data Recode window.

Endogenous three-category variables

To see the category boundaries do not matter for a three-category endogenous variable, suppose that Y in the following model is a three-category ordinal variable.

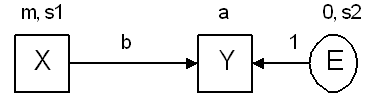
Suppose that you have estimated the model parameters after assigning values 3 and 4 to the two boundaries that separate the three categories. Now suppose that you change the two boundary values to another pair of values, say 0 and 100. This amounts to a re-scaling of the underlying numeric variable that is associated with Y, where first the unit is changed by multiplying every score by 100, and then the origin (zero point) of the underlying variable is changed by subtracting 300 from every score:

new Y score = (old Y score) × 100 - 300

This re-scaling of the underlying variable associated with Y can be compensated for by modifying the model parameters as follows.

▪First, multiply the regression weight, b, by 100.

▪Then, subtract 300 from the intercept, a.

This shows that for an endogenous variable the boundaries 0 and 100 are just as good as the boundaries 3 and 4. In other words, one pair of boundaries is as good as another, at least as long as a and b are unconstrained.

Exogenous three-category variables

To see that the boundary values do not matter for a three-category exogenous variable, suppose that X in the above model is a three-category ordinal variable. Suppose that you have estimated the model parameters after assigning values 3 and 4 to the two boundaries that separate the three categories. Now suppose that you change the two boundary values to another pair of values, say 0 and 100. This amounts to a re-scaling of the underlying numeric variable that is associated with X, where first the unit is changed by multiplying every score by 100, and then the origin (zero point) of the underlying variable is changed by subtracting 300 from every score:

new X score = (old X score) × 100 - 300

This re-scaling of the underlying variable associated with X can be compensated for by adjusting the model parameters as follows.

▪First, multiply the variance, s1, by 10,000 (i.e., 1002).

▪Then, subtract 300 from the mean, m.

This shows that for an exogenous variable the boundaries 0 and 100 are just as good as the boundaries 3 and 4. In other words, one pair of boundaries is as good as another, at least as long as s1 and m are unconstrained.

Several variables measured using the same three categories

It can happen that two or more measured variables use the same three categories. In that case, it may be appropriate to use the same category boundaries for each variable, even though the specific values do not matter. For example, suppose that in the following model, X1, X2, X3 and X4 are are responses to the same questionnaire item at four time points.

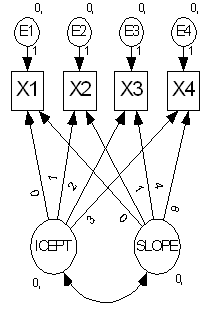
If X1, X2, X3 and X4 are ordinary numeric variables, then you would use the same measurement scale for all four. For example, if X1, X2, X3 and X4 were all measurements of length, you would use centimeters for all four measurements, or inches for all four measurements, but you would not mix different measurement scales. Similarly, if X1, X2, X3 and X4 are categorical variables, you would use the same category boundaries for all four variables.