IBM® SPSS® Amos™ 28
Speeds up the bootstrap algorithm and makes it more reliable under the assumption that standard errors are inversely proportional to the square root of sample size.
Syntax
object.BootFactor (M)
The BootFactor method syntax has the following parts:
Part |
Description |
object |
An object of type AmosEngine. |
M |
A positive integer. In the BootFactor example, M=5. Suppose that your data consist of G independent samples (groups) with sample sizes
|
Placement: [1].
Default
M = 1.
Remarks
Using a value for M other than 1 requires the assumption that the standard error of each estimate is inversely proportional to the square root of sample size.
The use of M > 1 can substantially reduce computation time, and reduces the probability of encountering a bootstrap sample for which parameter estimation is impossible. The larger M is, the larger the bootstrap samples will be, the more closely their sample moments will resemble the moments of the original sample, and the more closely the parameter estimates for the bootstrap samples will resemble the parameter estimates from the original sample. Since the parameter estimates from the original sample are used as initial values in the analysis of each bootstrap sample, a large value for M reduces the amount of computation required to estimate parameters for a bootstrap sample. Of course, if M is set to a very large value, generating the bootstrap samples will become the dominant cost factor. A very large M may also create numerical problems.
The use of M > 1 solves a problem described in a special case by Dolker, Halperin and Divgi (1982). With small samples and M=1, the sample covariance matrix in a bootstrap sample may be singular even though the covariance matrix in the original sample is nonsingular. The occurrence of a singular covariance matrix in a bootstrap sample prohibits estimation by the Gls or Adf methods. The larger M is, the smaller are the chances of finding a singular sample covariance matrix in a bootstrap sample.
It is not possible to perform a Bollen-Stine bootstrap test of fit or to obtain bootstrap confidence intervals (ConfidenceBC or ConfidencePC) if M >1.
See Also
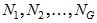 . Each bootstrap sample will be obtained from the original sample by drawing
. Each bootstrap sample will be obtained from the original sample by drawing 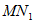 observations at random (with replacement) from the first original sample,
observations at random (with replacement) from the first original sample, 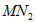 observations from the second original sample, and so on. As an example, suppose you have two independent groups with 200 cases in the first group and 250 cases in the second group, and that
observations from the second original sample, and so on. As an example, suppose you have two independent groups with 200 cases in the first group and 250 cases in the second group, and that 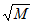 .
.