IBM® SPSS® Amos™ 28

An ordered-categorical variable with only two categories requires additional parameter constraints to make the model identified, beyond the constraints that would be required if the dichotomous variable were instead numeric. With two categories, there is only a single category boundary. That boundary can be fixed at a constant, but that is not enough to determine both the origin and scale for the underlying numeric variable. One more constraint is needed, and that constraint can only be imposed on the model parameters associated with the two-category variable.

Exogenous dichotomous variables

If a two-category variable is exogenous, any one of the following can in principle be fixed at a constant in order to determine the scale of the underlying numeric variable. (This is not an exhaustive list.)

▪The variable's mean

▪The variable's variance

▪The regression weight corresponding to a single headed arrow pointing away from the variable.

The choice of which parameter to fix at a constant can affect the speed with which the MCMC algorithm converges. Experience shows that the MCMC algorithm performs best when the variable's variance is fixed at a constant.

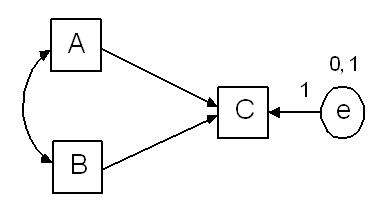
As an example, take the following path diagram.

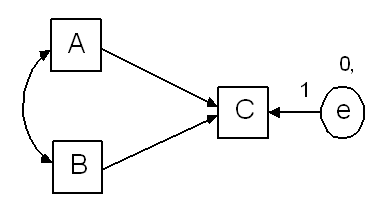
If A, B and C are numeric variables, then this model is identified. (Two parameters have been set equal to constants in order to overcome indeterminacy in the origin and unit of measurement of e.) If any of A, B, and C are ordered-categorical variables with three or more categories, the model is identified as well. But suppose A is dichotomous. Then an additional parameter constraint is required in order to make the model identified. Following the recommendation above, we fix the variance of A to a constant, as follows.

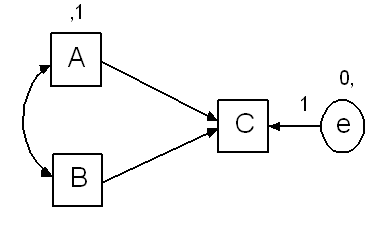
Endogenous dichotomous variables

If the two-category variable is endogenous, any one of the following can in principle be fixed at a constant in order to determine the scale of the underlying numeric variable. (Again, this is not an exhaustive list.)

▪The variable's intercept

▪The variable's error variance

▪The regression weight corresponding to a single headed arrow pointing to or from the variable.

The choice of which parameter to fix at a constant can affect the speed with which the MCMC algorithm converges. Experience shows that the MCMC algorithm performs best when the variable's error variance is fixed at a constant.

To illustrate this method of identifying a model, start again with the following model, which is identified as long as A, B and C are numeric or are ordered-categorical with three or more categories.

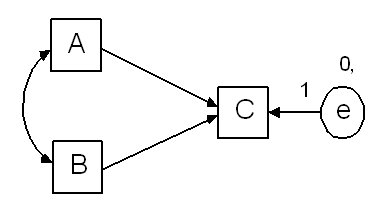
Now suppose that C is dichotomous. Then an additional parameter constraint is needed in order to make the model identified. Following the above recommendation, we set the variance of e to a constant, as follows.