IBM® SPSS® Amos™ 28

With more than three ordered categories, Amos estimates the category boundaries by assuming that the underlying numeric variable is normally distributed. If you do not assign values to any of the category boundaries ahead of time, Amos assumes that the underlying numeric variable has a mean of 0 and a standard deviation of 1. An example will show how that is done. Suppose that an ordered-categorical variable has four possible responses, Low, Medium, High and Very High, that were observed with the following frequencies.

Then the three category boundaries are estimated as follows.

The boundary between Low and Medium is estimated as -1.811 because 3.51% of the area under the standard normal curve lies to the left of -1.811. The boundary between Medium and High is estimated as -.022 because 45.61% of the area lies between -1.811 and -.022. The boundary between High and Very High is estimated as .80 because 29.82% of the area lies between -.022 and .805.

You can assign values to one or two category boundaries by clicking the Details button in the Data Recode window. If you specify a value for a single boundary, Amos adjusts the other boundaries so that the underlying numeric variable is normally distributed with a standard deviation of 1, but not necessarily a mean of 0. In the above example, if you specify a value of 0 for the boundary between Low and Medium, a constant 1.811 will be added to the boundaries given above, resulting in the following boundaries.

If you specify a value for two boundaries, Amos adjusts the other boundaries so that the underlying numeric variable is normally distributed with mean and standard deviation chosen so as to give boundaries that have the values that you specified. For example, if you specify that the boundary between Low and Medium is 0 and the boundary between Medium and High is 1, then the third boundary is adjusted as follows.

This method for choosing category boundaries is inappropriate for some models

When an ordered-categorical variable has more than three categories in a mixture modeling analysis, Amos cannot estimate values for the category boundaries. Values are arbitrarily assigned to the boundaries by assuming that measurements are normally distributed when the groups are pooled together. However, this assumption is expected to be violated in a mixture modeling analysis. Therefore, it is important to enter boundary values by clicking the Details button in the Data Recode dialog for any ordered-categorical variable that has more than three categories. As suggested below, an alternative solution is to combine categories in order to reduce the number of categories to three.

Some models imply that an underlying numeric variable is not normally distributed, and in that case Amos's method for choosing boundaries is incorrect if that variable has more than three categories. This will occur when a variable with more than three categories depends directly or indirectly on an observed exogenous variable that is not normally distributed. The following path diagram shows an example.

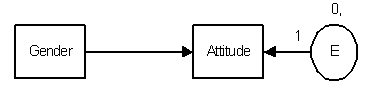
Suppose that Attitude is an ordered-categorical variable with more than four categories, say Strongly disagree, Disagree, Agree, and Strongly agree. The important thing for this example is that it has more than three categories, so that Amos assumes that its underlying numeric variable is normal for purposes of estimating the category boundaries. But suppose that E is normally distributed while Gender is a dichotomous variable that is scored 0 and 1. Then Attitude's underlying numeric variable (which depends linearly on Gender and E) will have a bimodal distribution. Boundary estimates that assume that Attitude is normally distributed will be wrong.

Amos's method for estimating boundaries for variables that have more than three categories can also give incorrect boundaries when multiple variables use the same categories and are required to have the same boundary values. For example, suppose that in the following model, X1, X2, X3 and X4 are are responses to the same questionnaire item at four time points.

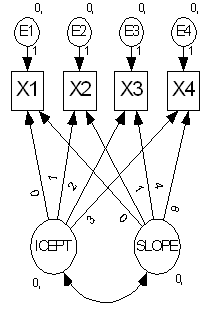
It is important to use the same category boundaries for X1, X2, X3 and X4 . However, Amos provides no mechanism for doing so when the questionnaire item has more than three possible responses.

When an ordered-categorical variable has more than three categories, and the model implies that the underlying numeric variable is not normally distributed, or the category boundaries need to be the same for multiple variables, some consideration should be given to combining categories in order to reduce the number of categories to three, particularly if some of the categories occur with low frequency.